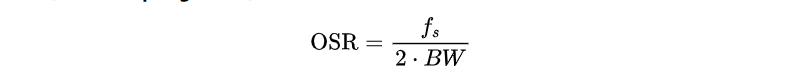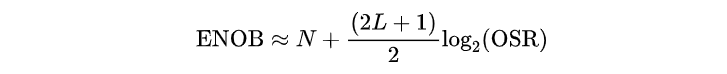大家好,简单分享下
事实上ADC 的 ENOB(有效位数)、采样率(Sampling Rate, )和过采样比(OSR, Oversampling Ratio)之间存在密切关系,尤其是在 Σ-Δ ADC 或使用 数字后处理(如滤波+平均) 的系统中(因为SAR,流水线这些没有这样的设计):
基本定义
ENOB(Effective Number of Bits) :表示 ADC 实际分辨率,考虑了噪声和非理想因素后的有效位数。
OSR(Oversampling Ratio) :
其中 BW 是信号带宽, f
s是采样频率。OSR 越大,表示在固定信号带宽下使用更高采样率。
ENOB 与 OSR 之间的理论关系
对于 Σ-Δ ADC:
在理想情况下,Σ-Δ ADC 的 ENOB 随 OSR 增大而提升,满足如下近似关系:
其中:
N:ADC 本身的量化位数(例如 1 位、5 位 Σ-Δ)
L:Σ-Δ 调制器的阶数(1 阶、2 阶、3 阶…)
BSR:过采样比
这是因为 Σ-Δ ADC 的噪声整形效应 会将量化噪声推向高频,配合数字滤波器有效滤除,从而提升低频段 SNR 和 ENOB。
对于一般 ADC + 数字平均/滤波系统:
当使用常规 SAR ADC(无噪声整形),但采用后端滤波或平均时,ENOB 提升主要来自白噪声功率被平均 :
或者:
因此,每增加 4 倍 OSR,ENOB 理论上提升约 1 位(6 dB SNR 提升)。
三者之间总结关系表格
| 参数变化 |
对 ENOB 影响 |
说明 |
| 增大采样率 (固定带宽) |
↑ |
增大 OSR,白噪声平均或噪声整形更有效 |
| 增大 OSR(固定带宽) |
↑ |
ENOB 提升,Σ-Δ 最明显,SAR 较次 |
| 增大带宽(固定采样率) |
↓ |
OSR 减少,ENOB 下降 |
| 提升 Σ-Δ 阶数 |
↑↑ |
ENOB 增长更快,对 OSR 更敏感 |
可视化一下 ENOB 与 OSR 的关系(Σ-Δ 2阶调制器):
可视化一下 ENOB 与 OSR 的关系(Σ-Δ 2阶调制器):
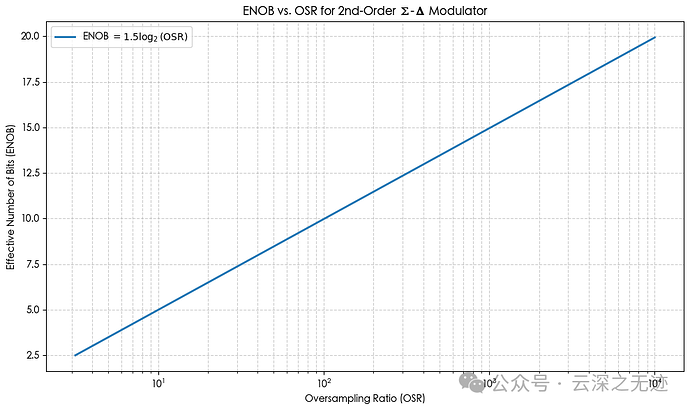
会看到一个对数曲线:每翻倍 OSR,ENOB 增长约 1.5 位。
图: ENOB 与 OSR 的对数关系
每当 OSR 翻倍,ENOB 增加约 1.5 位;曲线是
对数增长 ,说明在高 OSR 区间,ENOB 增长趋于缓慢。
这符合二阶 Σ-Δ 的理论性能:过采样 + 噪声整形每倍增 OSR 带来 6 dB × 1.5 = 9 dB 的 SNR 增益,即提升约 1.5 bit 的 ENOB。
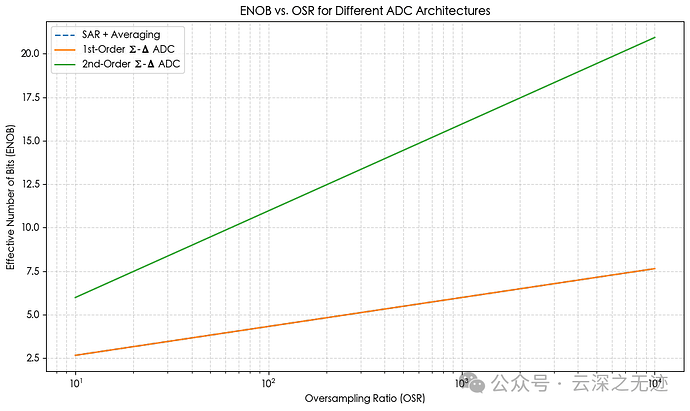
图:ENOB 随 OSR 增长的趋势
对比了三种典型情况:
SAR + Averaging(虚线) :ENOB 每增加 4× OSR 提升 1 位(6 dB);
1阶 Σ-Δ ADC :与 SAR 相同的增长速率;2阶 Σ-Δ ADC :每增加 4× OSR 提升约 1.5 位,具有更显著的噪声整形效果。
这说明:在高 OSR 条件下,Σ-Δ 架构能更有效地提升分辨率,尤其适用于低带宽高精度应用。
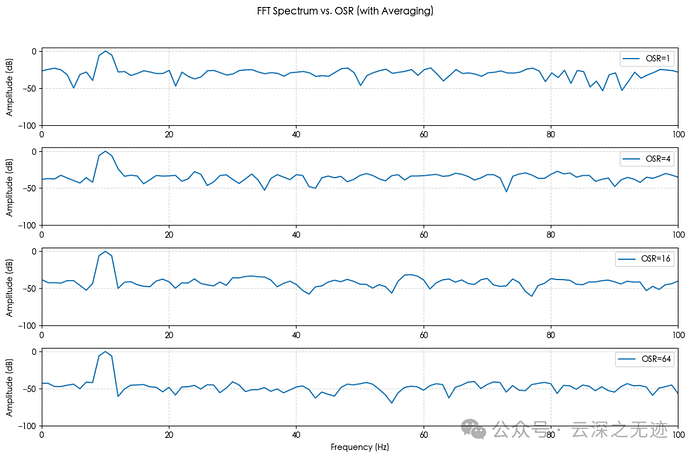
图:在不同 OSR 条件下(1×、4×、16×、64×)的 FFT 频谱图
OSR = 1(未过采样) :背景噪声较高,信号峰值与噪声底之间差距较小;随着 OSR 增大 ,信号峰值保持不变,但噪声底明显下降 ,这意味着 SNR 和 ENOB 得到了提升;滤波器效果模拟为移动平均 ,其带宽随 OSR 收窄,有效滤除了高频噪声成分。
过采样 + 滤波可以大幅降低宽带噪声;ENOB 提升本质来自信噪比(SNR)提升;与理论曲线一致,每 4× OSR 提升约 6 dB SNR ,即 1 位 ENOB。