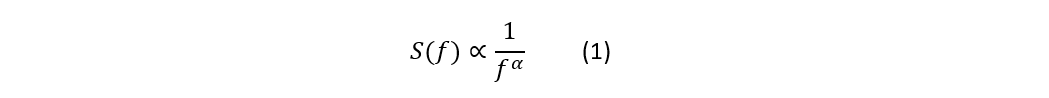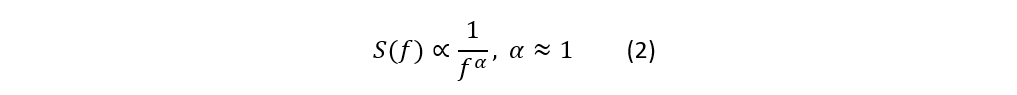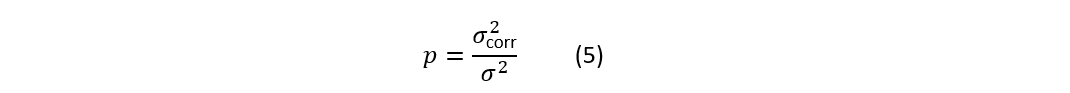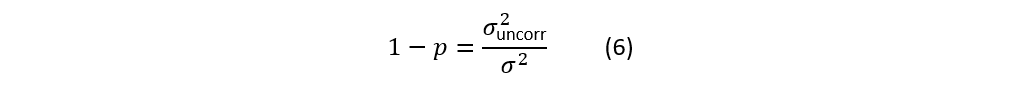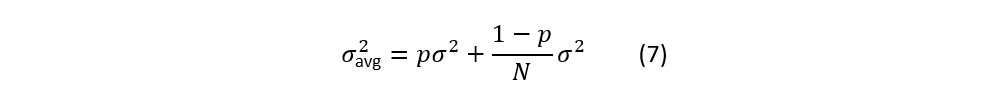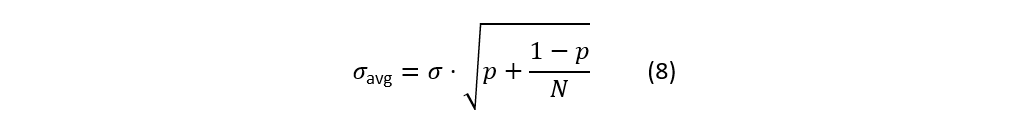在信号处理里说的 “粉红噪声 (1/f noise)” 的“粉红”其实只是一个类比名称,并不是真的在可见光意义上的粉红色,而是来源于频谱能量分布和可见光颜色的类比。
颜色类比的由来
白噪声:频谱密度在所有频率上都相同(平坦 PSD),类比为“白光”含有所有可见光波长;功率谱密度(PSD)在频域中是常数,不随频率变化,单位通常是 V²/Hz 或 nV/√Hz。
粉红噪声 (1/f):功率谱密度随频率成反比衰减,即低频成分多,高频成分少;类比为“粉红光”中低频(红色端)成分较多,高频(蓝色端)成分较少。
棕噪声 (1/f²):低频成分更占优势,频谱偏向“棕色”。
粉红噪声的功率谱密度:
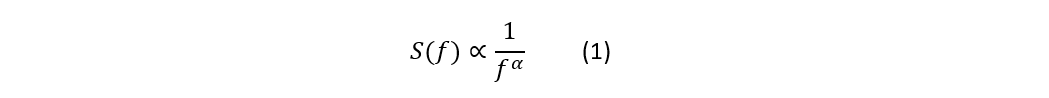
其中
α = 1 → 粉红噪声
α = 0 → 白噪声
α = 2 → 棕噪声
粉红噪声(Pink Noise)/ 1/f 噪声:功率谱密度与频率成反比,
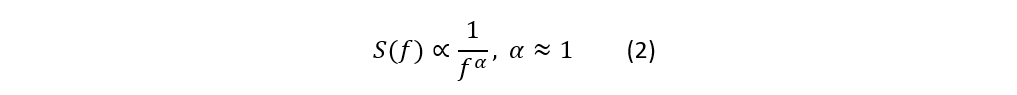
所以低频部分噪声幅度更大,高频部分逐渐衰减。
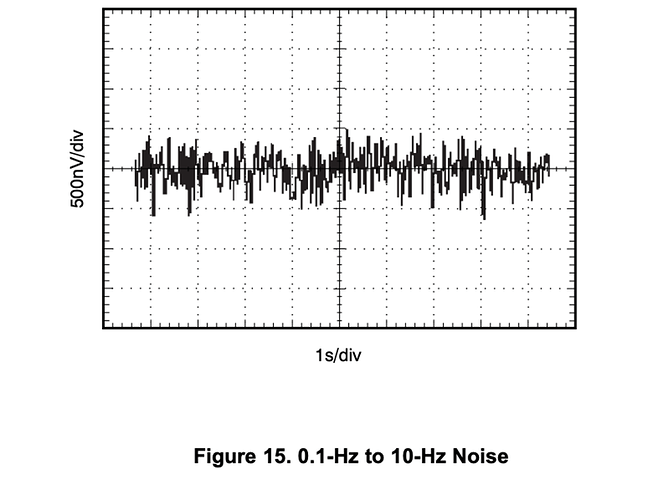
在精密基准、ADC、运放等模拟器件里,低频区域的噪声几乎总是 1/f 型的,这部分会显著影响 低带宽测量(例如 0.1–10 Hz 噪声指标就是专门衡量它的);在音频工程领域,“粉红噪声”通常指 α=1 的情况,而 1/f 噪声有时 α 会略偏离 1,比如 0.8~1.2。
上面这种图也多,但是一些器件会给下面的样子:
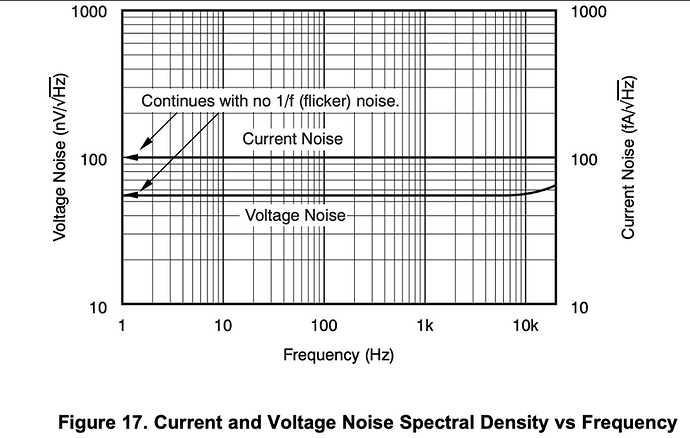
图是
运放的电压噪声和电流噪声谱密度(Spectral Density)随频率变化的典型规格图,纵坐标是对数刻度,横坐标是频率(Hz),左右两侧分别标出了电压噪声(nV/√Hz)和电流噪声(fA/√Hz)。
电压噪声(Voltage Noise)
用左边纵坐标(nV/√Hz)表示。
从低频到高频几乎是水平直线,说明该器件没有 1/f 闪烁噪声(flicker noise),低频区域噪声谱密度不随频率上升;在高频(>10 kHz)有轻微上升,这通常是运放带宽和输入结构造成的。
电流噪声(Current Noise)
用右边纵坐标(fA/√Hz)表示;同样在全频段保持近似常值,没有低频 1/f 上升,表明输入偏置电流噪声也非常稳定。

共同特征
两条曲线都有标注 “Continues with no 1/f (flicker) noise”,强调白噪声主导,无明显低频噪声膨胀;这种噪声特性对精密低频测量非常有利,因为 1/f 噪声会在低频累积,影响 DC~Hz 级别的信号测量。
在 1~10 Hz 区域,很多普通运放的电压噪声会随 1/f 增长(例如 +10 dB/decade),而该器件保持平坦,意味着低频测量稳定性非常高;对于精密测量(如高分辨率 ADC、传感器前端),这种特性可显著降低低频漂移。
电压噪声与电流噪声分开标注,设计者可根据输入阻抗来判断哪种噪声占主导:
高阻源(如传感器电阻 >100 kΩ):电流噪声影响更大
低阻源(<1 kΩ):电压噪声影响更大
单位的物理意义
nV/√Hz 或 fA/√Hz 表示的是噪声谱密度(Power Spectral Density 的平方根),可用于计算带宽内的等效 RMS 噪声:

与 1/f 噪声比较
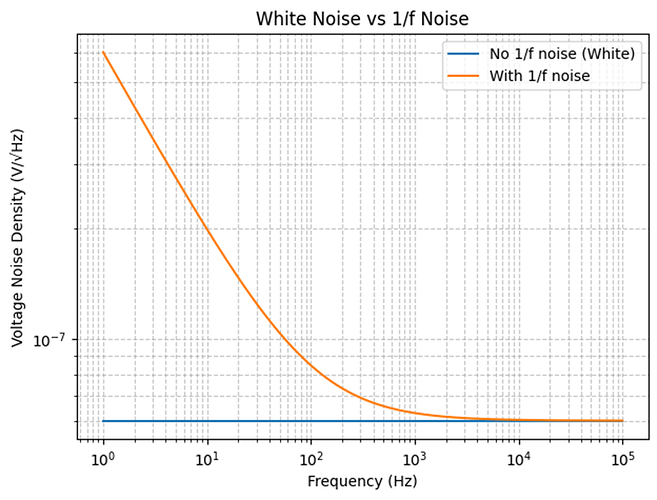
如果存在 1/f 噪声:在低频区(<100 Hz)曲线会陡峭上升(斜率 -10 dB/decade)。
需要计算一个拐点频率(f_corner),低于该频率 1/f 占主导,高于则白噪声占主导;而这里的曲线几乎无拐点,说明白噪声主导全频段。
蓝色曲线(No 1/f):和你图中一样,低频到高频几乎平坦。
橙色曲线(With 1/f):低频明显上升,拐点频率处开始变平,我手上那张数据手册图对应的就是蓝色曲线。
听感 & 视觉化
听感:粉红噪声听起来比白噪声更“温和”,低频更厚重,不像白噪声那么尖锐刺耳。
可视化颜色:如果用频谱颜色映射来渲染信号,粉红噪声的频谱会在低频一端(红区)亮一些,高频(蓝区)暗一些,因此整体呈现偏暖色调,看上去有“粉色感”。
在一些音频软件的瀑布图中,粉红噪声的频谱倾斜 10 dB/倍频程,看起来像是一条从左上到右下的斜线。
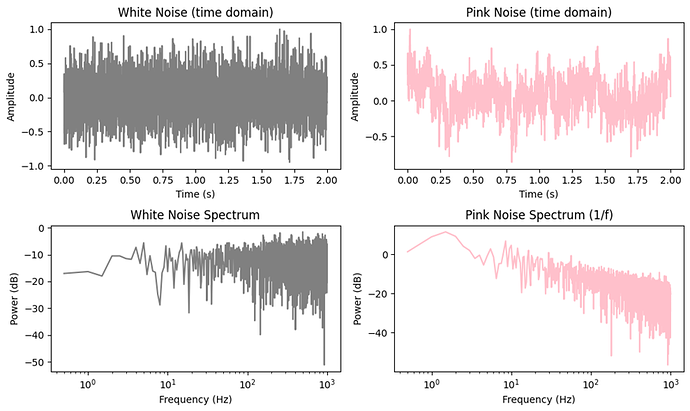
白噪声的时域波形(灰色)和频谱(平直)
粉红噪声的时域波形(粉色)和频谱(低频能量高,~1/f 下降)
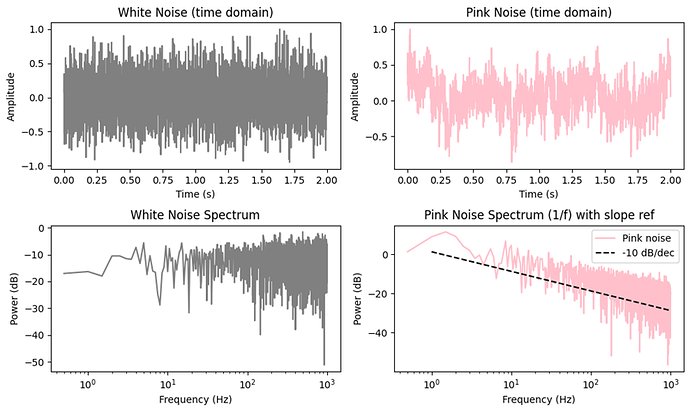
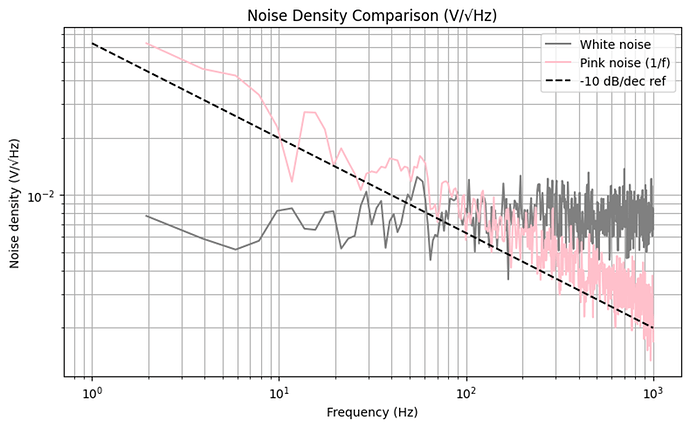
粉红噪声频谱 会有一条黑色虚线参考斜率 (-10 dB/dec),和你的数据对比非常直观;能直接验证低频段是否符合 1/f 特性,高频段是否趋于平坦(白噪声部分)。
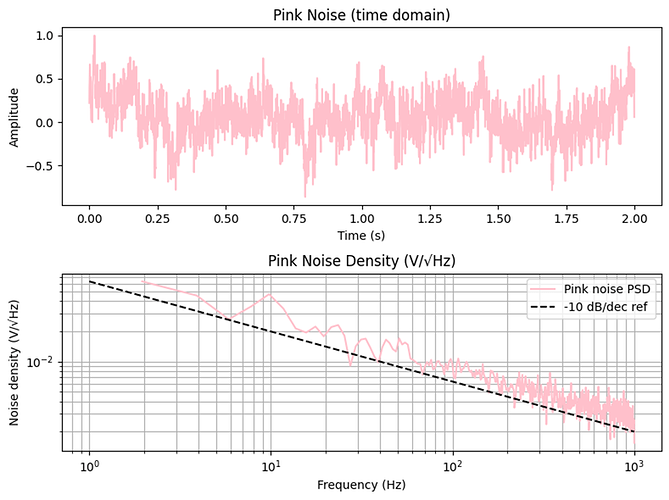
时域波形(方便直观感受幅度和随机性)
功率谱密度曲线(单位是 V/√Hz,低频随 1/f 上升,高频趋于平坦)
-10 dB/dec 参考虚线(用于验证粉红噪声的理论特性)
白噪声曲线几乎在整个频段内平坦
粉红噪声曲线在低频段随频率下降呈 1/f 上升趋势
虚线是 -10 dB/dec 的理论参考
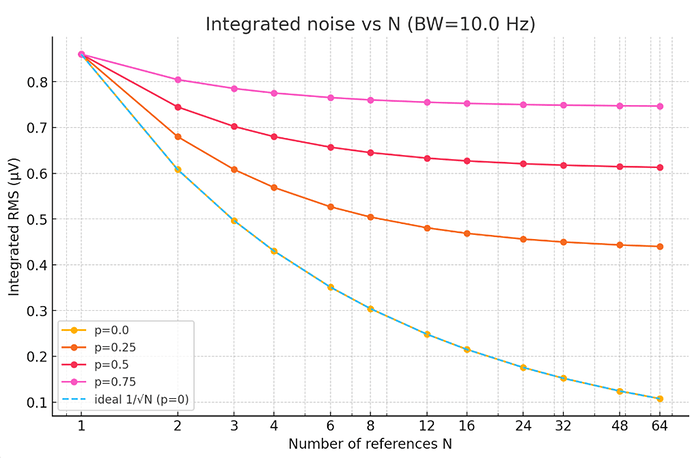
在 BW=10 Hz 下,RMS 随 N 的曲线,对比“理想 1/√N”与 p≠0 的实际曲线。
理想情况下(各基准噪声完全不相关),并联平均的 RMS 噪声按 1/√N 下降。
只要存在部分相关(例如同一电源纹波、PCB 热-机械耦合、相邻芯片的低频漂移),下降会变钝:RMS ∝ √(p + (1–p)/N)。
这里:p 是“共同噪声占比”的等效相关度(0=全不相关,1=全相关)。
- p=0 → 理想 1/√N;
- p=0.25 → N→∞ 时只能降到 √0.25=0.5(也就是最多改善 2×);
- p=0.5 → 天花板是 0.707(最多 1.41×);
- p→1 → 几乎没有收益。
1/f 区(超低频)更容易出现“看起来不像 1/√N”:
因为
(a) 每颗芯片的 1/f 噪声在极低频段“慢到像漂移”,窗口内样本有限,统计不稳定;
(b) 有相当一部分是共模源(温漂、应力、PSRR 不足引入的电源纹波),等价于上面的 p>0。
所以在 0.1–10 Hz、1 Hz ENBW 这类窗口里,经常会看到曲线比理想直线更平、且不同批次差异很大。
这里的 p 指的就是共同噪声功率占比(power fraction of correlated noise),可以理解为一个“等效相关度系数”,范围在 0 到 1 之间:
p = 0 → 各通道的噪声完全独立(无任何相关成分),并联平均后可以达到理想的 1/√N 降噪;
p = 1 → 各通道噪声完全相同(100% 相关),平均完全没有效果,RMS 不下降;
0 < p < 1 → 只有部分噪声是相同的,部分是独立的,降噪效果会介于这两者之间。
数学解释
假设每路的总噪声功率 σ^2 可分成两部分:
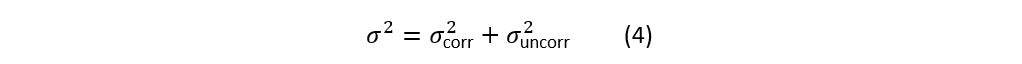
共同噪声功率比例:
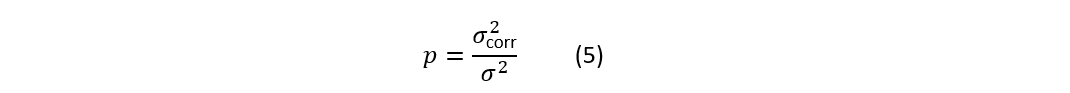
独立噪声功率比例:
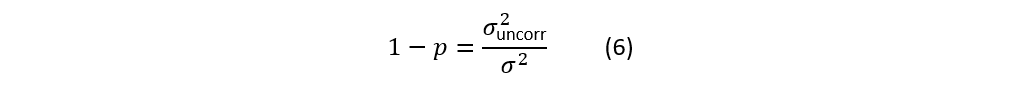
当 N 路平均时:共同噪声部分不会被平均,功率保持不变;独立噪声部分会按 1/N 衰减。
于是并联平均后的总噪声功率:
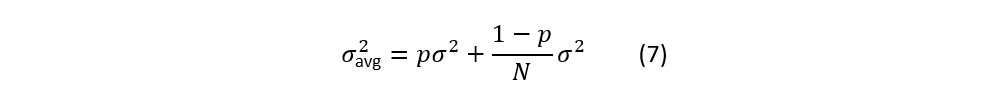
所以:
如果单个基准的 RMS 噪声是 1 µV:
p = 0,N=4 → RMS = 1/√4=0.5µV(理想降噪)
p = 0.25,N=4 → RMS = 1⋅√(0.25+0.75/4)≈0.612µV(效果变差)
p = 0.5,N=4 → RMS = ≈0.707µV(收益更小)
p = 1,N=4 → RMS = 1.000 µV(无收益)