【热情分享】5000字细品这篇1997年国际计量局大佬的信号链古早论文（低频相关）

资源中心
1

寒冷冬季古早论文暖人心！今天就向论坛的坛友们分享一篇1997 的 IEEE 论文！

image
image875×609 124 KB

法国的数学是和俄罗斯比肩的存在，嘎嘎硬，先贴上一篇大佬镇楼。

至于为什么我要写这个，是因为这个文章在数学层面证明了一些测量的极限：

image
image875×292 64 KB

我先通俗的解读一下，然后再展开证明。这篇论文的数学不是“为了算而算”，而是把“直流/低频测量到底受什么限制、该测多久、该不该平均、平均有没有用”这些工程决策问题，变成可计算、可验证的规则。

2

它解决的核心问题是什么？

当在测 nV～µV 级直流或低频信号时：看到的波动，到底是
仪器本身的噪声？你的滤波/积分方式？环境周期干扰？1/f 漂移？温度系数？还是“平均方法用错了”？可贵之处就是在于这篇论文的数学 = 一套“判责工具”。
告诉仪器“真正的有效带宽 B”是多少？
不是手册写的，也不是设置的 PLC / filter 档位，而是 实际对噪声起作用的 ENBW，通过公式：

B=(∫G_xx (f) df)/(G_xx (0) ) （1）

仪器要测多久才有用？
论文给出的关键结果：

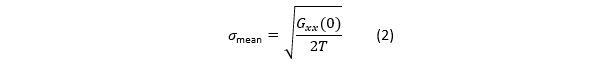
image
只要低频是白噪声 ，最终均值精度 只取决于：低频噪声密度 和总测量时间 ，与怎么调滤波器、PLC、积分次数无关。

如果已经在白噪声区，再“调慢读数 / 加大平均 / 调更窄带宽”，不会让最终结果更准，只会等得更久。这对任何“长期稳定性测量”都是颠覆性的结论。

3

“判断“平均到底有没有用？

论文给出一个非常实用的判据：

f≳1/Tmeas

如果在Gxx (f)的频段内， 是常数（白噪声），那这些数据来自同一统计总体，可以直接平均。

否则会出现 1/f，出现低频峰，出现漂移，那这个时候直接平均 = 自欺欺人 ，这比“看时间曲线抖不抖”可靠得多。

区分是谁在制造噪声？

通过 PSD 形态可以分辨：

频谱形态 含义
平坦 白噪声（仪器/热噪声极限）
漂移、温度、参考源本征
窄峰 工频 / 空调 / 周期扰动
roll-off 滤波器 / 积分行为

image
image875×231 57.3 KB

论文用这一方法证明 标准电池几乎没有低频噪声，证明 Zener 基准的低频噪声显著 ，最终定位出 温度系数是根因。

不是“多少 µVpp”，而是“频率结构”！

低频性能不是一个数值，而是一条谱。这直接否定了：“这颗基准噪声是 1 µVpp”，“这台 ADC 很稳，看起来不漂”这些说法。**真正决定能不能用的是：**在你关心的频段内，PSD 是不是白的，1/f 拐点在哪里。

开始证明

在证明前会用标准信号处理记号重写一遍，但含义与论文一致。 先统一记号

先统一记号

image
image571×181 4.39 KB

式(1)：用分段平均估计 PSD

论文按 Bendat & Piersol 的方法：把长数据切成 n_d 段（records），每段长度 T，对每段做有限时长傅里叶变换，然后对“段功率谱”取平均得到 PSD 估计，可以把式(1)理解为下面这种形式（等价的）：
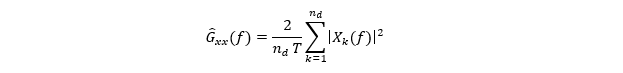
image
Xk (f)：第 k 段数据在区间长度 T 上的有限傅里叶变换（单位：V·s）；前面的 2/T 来自单边谱的约定（把负频率能量折算到正频率）。
每一段给一个 noisy 的谱估计；对多段平均能降低谱估计的随机波动（方差）；其中低频分辨率由 T 决定：最低频点大约是 1/T。这就是为什么作者关心到 5 mHz，需要记录到几百秒乃至小时量级。
要看更低频：加长 T（记录更久）。
要谱更平滑：增大段数 nd（更长总时间或更多重叠），论文里每个谱取 7 段平均。

式(2)：PSD 积分 = 均方值（Parseval 的随机过程版本）

论文式(2)说：PSD 与 的均方值（mean square）满足
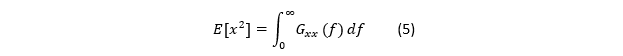
image
把“频域的噪声密度”与“时域的 RMS/方差”直接连起来；如果 G_xx (f) 在某个频带里高，那说明该频带对时域方差贡献大，所以想降 RMS，不一定盲目加平均；先看是哪段频率在贡献能量，然后针对性滤波/隔离/建模。
单边/双边
双边 PSD（-∞ 到 +∞）与单边 PSD（0 到 +∞）差一个 2 的约定，论文在式(1)已明确使用“one-sided PSD”。

image
image875×199 56.2 KB

式(3)：噪声谱带宽 的定义（等效矩形带宽 ENBW）

论文定义“噪声谱带宽”：
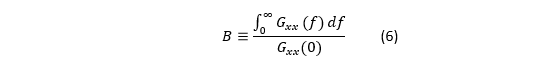
image
其中 Gxx (0) 是 PSD 在零频附近的极限值（白噪声平台高度）。
为什么这是“带宽”？
如果输入是白噪声：Gxx (f)=G0（常数），经过一个低通系统后，输出 PSD 变成 G0 |H(f)|^2，那么输出均方值：
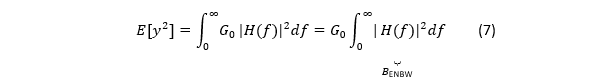
image
而式(3)做的正是把这个积分“等效”为一个矩形低通：高度 G_xx (0)=G_0，宽度 B；所以 B 就是等效噪声带宽（ENBW）。

论文怎么用它算 RMS

image
image875×629 40.2 KB

先在滤波 roll-off 之前的频率范围取 Gxx (f) 的平均，作为 Gxx (0) 估计；再用积分（实际是频点求和）得到 ∫Gxx (f)df；得到 B≈0.031 Hz，并算出标准差约 3.7 nV。
不必相信仪器手册“滤波档位=多少 Hz”，可以用谱把实际带宽反推出。

4

Nyquist 热噪声：用“已知平坦 PSD”标定仪器

论文用理想电阻的热噪声作为已知输入 PSD：
image
这构造了一个“平坦、可计算”的噪声源，用来测纳伏表的频率响应与带宽。
为什么能反推出仪器频响？
把纳伏表视作线性系统 H(f)（包含模拟/数字滤波、积分等）：
image
论文在式(1)后面就给了这个关系（输入 PSD、输出 PSD 与传递函数的关系）。
因此：
image
这样就能从测得的输出 PSD 直接得到 H(f) 的形状（至少是幅度平方），再进一步求 ENBW，这也是作者先接 1300 Ω 电阻做“基础构造”的原因。
“1/B 的测量时间”从哪里来？（统计独立性与白噪声假设）
论文在图1后面给了一个非常实用的结论：要让测量结果“像来自同一统计总体”，测量/平均时间需要至少到 ∼1/B 的量级，因为这是仪器等效滤波的 settling/相关时间尺度。
更细一点：作者引用更严格的处理指出，在白噪声且采样率远大于带宽时，时间间隔约 1/(2B) 的样本近似不相关；低通滤波器会让相邻读数相关；相关长度约等于滤波器脉冲响应的“有效长度”，而 ENBW 与这个时间尺度互为倒数关系（粗略来说）。
式(4)：均值的标准差 σm 与 Gxx (0)、测量时间 T 的关系
论文给出的“有趣结果”：
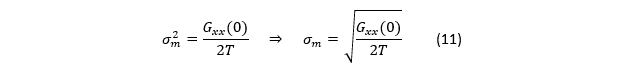
image
在白噪声前提下：每个“独立样本”间隔约 1/(2B)；总测量时间 T 内独立样本数约 N≈2BT；单次读数方差（输出方差）约 σ^2≈Gxx (0) B（来自式(2)(3)：白噪声平台 × ENBW）；均值方差为 σm^2=σ^2/N≈(Gxx (0)B)/(2BT)=Gxx (0)/(2T)。
注意：这里B 被消掉了，这就是作者说“interesting result”的原因：
在白噪声极限下，把滤波器调得更窄（B 更小）会让单次读数更稳，但同时独立样本来得更慢；两者抵消后，最终均值不确定度只取决于 G_xx (0) 与总时间 T。
如果确认低频段是白噪声平台（Gxx (f) 常数），那就要把均值标准差降一半，就需要把总测量时间增大 4 倍（因为 σm∝1/√T）；调滤波档位（改变 B）对“最终均值精度”未必有用，它更多影响的是“读数更新率与瞬时波动”。真正决定均值精度的，是低频白噪声平台高度 Gxx (0)（也就是系统底噪密度）。

5

适用条件是什么？

式(4)只在以下条件成立时才可靠：低频是白噪声（无明显 1/f、漂移、温度循环峰）；采样率远高于带宽；系统近似线性、稳态。

若存在漂移/1/f，作者也明确说要用极性反转或漂移模型修正，否则“直接平均”会错。 （这一看就散会）

Table I 的数学：G_xx (f)∝1/f^a 的拟合

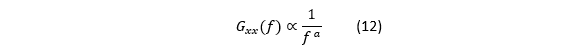
image
image875×191 18.7 KB

表 I 用幂律拟合低频 PSD：
image
在低频时这很典型：
a≈1 是经典 1/f 噪声；
a<1 表示比 1/f “更平缓”；
更低频若出现“漂移/温度循环”，谱会出现峰或更陡的趋势；作者列出不同 732B 在 1.018 V 与 10 V 输出下的 a、拟合频段、以及 Gxx (fmin) 的量级差异（不同机器可差到 7–10 倍 PSD）。

式(5)(6)：温度系数模型（外温 vs 内部热敏电阻）

作者最终用回归拟合得出温度相关性，并给两种自变量：

用外部温度 （摄氏）

image
即“线性 + 二次项”。

用内部热敏电阻 （更贴近内部温度）

image
同样是二次形式。

为什么要两个温度？外部温度不一定等于基准内部关键节点温度；而且内部热敏电阻更接近“器件真正温度状态”，所以作者在结论里建议高要求场景用内部热敏电阻来校正。

工程化改造

明确要的指标（选一个）
瞬时读数标准差 （“抖动有多大”）
均值不确定度 σmean（“平均后有多准”）
低频噪声形态：白噪声/1/f/周期峰/漂移
明确频率范围（例如 10 Hz–5 mHz 对应 0.1 s–数小时量级）。

6

先“表征仪器”，再测被测件（DUT）

这是论文强调的关键顺序：先把纳伏表/采集链路的 实际带宽与滤波行为测出来，再去解释基准或样品的谱。

建立输入（任选其一，优先从简单到严格）

短路输入（看自噪）

高稳定电阻 R**（热噪声标定）**：电阻热噪声 PSD 近似常数，用来反推频响与带宽（论文用 1300 Ω）。

记录数据，时间戳 + 电压值（建议同时记录温度或内部热敏电阻值，如果有）；分析的时候做低频 PSD（分段/平均）：用 Welch（分段 FFT + 平均）等价实现论文式(1)。

从 PSD 推出“有效带宽 B”（ENBW）

找出低频“白噪声平台”高度 （不要取第一个点；用低频若干点的中位数/均值更稳）。

用论文式(3)定义计算
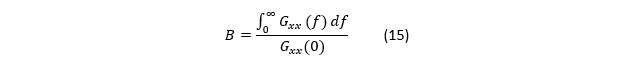
image
这就是“等效噪声带宽”，用于把各种滤波/积分/统计功能统一到一个可比较参数上。
决定“该测多久 / 平均是否有效”
判断能不能直接平均：看你关心的低频区 G_xx (f) 是否近似常数（白噪声）。如果出现明显 1/f 或漂移，应先做漂移处理（反转极性、拟合漂移、温度回归），再谈平均。
若白噪声成立，用论文式(4)直接规划总时长 T：
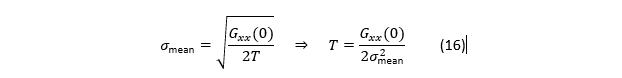
image
这一步是“从谱直接推测量时间”的核心产出。
对 DUT（基准/参考源）的测量与归因
DUT 评估建议做“差分测量”：DUT–参考，用纳伏表读差值（论文就是这么做标准电池 vs Zener）。 若低频出现“疑似温度引起的 1/f 或低频峰”：记录外部温度 θ 或内部热敏电阻 R，做回归拟合 V(θ) 或 V(R)（论文式(5)(6)是二次模型），把温度项扣除后再看 PSD 是否变“白”。
不要把趋势/漂移当噪声：PSD 会被最低频点“撑大”。建议先 detrend（去线性趋势）并对比“去趋势前后 PSD”；PSD 的第一个频点往往最不可靠（窗口、有限时长、漂移都会污染）；如果要到 mHz，记录时长必须是小时级（频率分辨率 Δf≈1/Tseg ）。

7

Python 模板
下面代码完成：
Welch PSD（单边）,估计 Gxx (0)（低频平台）
计算 ENBW B（式(3)离散积分）
用式(4)算 σmean或反算所需总时长 T
可选：去趋势、温度回归（线性/二次）

只需要把 t, x 换成你的数据（秒、伏）。

Estimated G0 (V^2/Hz): 5.0391599672716105e-17
Estimated ENBW B (Hz): 26.68274927928835
Sigma_mean for total time T (V): 3.415365594846628e-11
Time needed for target sigma_mean (s): 25.195799836358052   (~hours) 0.006998833287877237

CODE

import numpy as np

def detrend_linear(x: np.ndarray) -> np.ndarray:
    """Remove best-fit line to suppress drift leaking into lowest-frequency PSD bins."""
    n = x.size
    t = np.arange(n, dtype=float)
    A = np.vstack([t, np.ones(n)]).T
    k, b = np.linalg.lstsq(A, x, rcond=None)[0]
    return x - (k * t + b)

def welch_psd_onesided(
    x: np.ndarray,
    fs: float,
    nperseg: int,
    noverlap: int,
    window: str = "hann",
) -> tuple[np.ndarray, np.ndarray]:
    """
    One-sided PSD estimate (V^2/Hz) using Welch averaging.
    No scipy dependency; suitable for low-frequency work.
    """
    x = np.asarray(x, dtype=float)
    if noverlap >= nperseg:
        raise ValueError("noverlap must be < nperseg")
    step = nperseg - noverlap
    if x.size < nperseg:
        raise ValueError("x shorter than nperseg")

    # Window
    if window == "hann":
        w = np.hanning(nperseg)
    elif window == "rect":
        w = np.ones(nperseg)
    else:
        raise ValueError("Unsupported window")

    # Window normalization for PSD
    U = (w**2).sum()  # power normalization term
    scale = 1.0 / (fs * U)

    # Segment FFT accumulate
    nseg = 1 + (x.size - nperseg) // step
    acc = None

    for i in range(nseg):
        seg = x[i*step : i*step + nperseg]
        seg = seg - seg.mean()  # remove DC in each segment (helps low-f PSD robustness)
        X = np.fft.rfft(seg * w)
        Pxx = (np.abs(X) ** 2) * scale  # two-sided folded into rfft bins (not yet one-sided correction)
        if acc is None:
            acc = Pxx
        else:
            acc += Pxx

    Pxx = acc / nseg
    f = np.fft.rfftfreq(nperseg, d=1.0/fs)

    # Convert to one-sided PSD: double all bins except DC and Nyquist (if present)
    if nperseg % 2 == 0:
        # even: Nyquist bin exists at end
        Pxx[1:-1] *= 2.0
    else:
        Pxx[1:] *= 2.0

    return f, Pxx

def estimate_G0_from_lowband(f: np.ndarray, G: np.ndarray, f_lo: float, f_hi: float) -> float:
    """Estimate zero-frequency limit Gxx(0) using a low-frequency band median/mean."""
    mask = (f >= f_lo) & (f <= f_hi) & np.isfinite(G)
    if mask.sum() < 3:
        raise ValueError("Not enough points in lowband to estimate G0")
    # median is more robust against occasional peaks
    return float(np.median(G[mask]))

def enbw_from_psd(f: np.ndarray, G: np.ndarray, G0: float, f_max: float | None = None) -> float:
    """
    Compute B = integral(G df) / G0 using discrete trapezoidal integration.
    Optionally integrate only up to f_max to avoid irrelevant high-frequency tails.
    """
    if f_max is not None:
        m = (f <= f_max)
        f2, G2 = f[m], G[m]
    else:
        f2, G2 = f, G
    area = float(np.trapz(G2, f2))  # V^2
    return area / G0                # Hz

def sigma_mean_from_G0(G0: float, T_total: float) -> float:
    """Equation (4): sigma_mean = sqrt(G0 / (2T)) for white-noise regime."""
    return float(np.sqrt(G0 / (2.0 * T_total)))

def required_T_for_sigma_mean(G0: float, sigma_mean_target: float) -> float:
    """Rearranged equation (4): T = G0 / (2 * sigma^2)."""
    return float(G0 / (2.0 * sigma_mean_target**2))

def quad_regress(y: np.ndarray, x: np.ndarray) -> tuple[np.ndarray, np.ndarray]:
    """
    Fit y = c0 + c1*(x-x0) + c2*(x-x0)^2 (like paper eq(5)/(6)).
    Returns coeffs [c0, c1, c2] and fitted yhat.
    """
    y = np.asarray(y, float)
    x = np.asarray(x, float)
    x0 = float(np.mean(x))
    u = x - x0
    A = np.vstack([np.ones_like(u), u, u**2]).T
    c, *_ = np.linalg.lstsq(A, y, rcond=None)
    yhat = A @ c
    return c, yhat

# -------------------------
# Example usage (replace with your data)
# -------------------------
if __name__ == "__main__":
    # Suppose you have evenly-sampled data:
    fs = 1.0  # Hz (1 reading per second)
    T_total = 6 * 3600  # 6 hours
    N = int(fs * T_total)
    t = np.arange(N) / fs

    # Simulated signal: white noise + small 1/f-like drift component (for demo)
    rng = np.random.default_rng(0)
    x = 5e-9 * rng.standard_normal(N)  # 5 nV rms white component
    x += 50e-9 * np.sin(2*np.pi*(1/3600)*t)  # 1-hour environmental cycle (peak)

    # Optional: remove linear drift
    x_d = detrend_linear(x)

    # PSD
    nperseg = 4096
    noverlap = 2048
    f, G = welch_psd_onesided(x_d, fs=fs, nperseg=nperseg, noverlap=noverlap)

    # Estimate G0 in a low band that is ABOVE the very first bin and BELOW obvious roll-off
    # You must choose these based on your PSD shape; below is a typical starting point.
    G0 = estimate_G0_from_lowband(f, G, f_lo=2*(fs/nperseg), f_hi=0.02)  # e.g., 2 bins to 0.02 Hz

    # ENBW
    B = enbw_from_psd(f, G, G0=G0, f_max=0.5)  # integrate up to 0.5 Hz (adjust as needed)

    # Mean uncertainty (white-noise regime)
    sigma_m = sigma_mean_from_G0(G0, T_total=T_total)

    print("Estimated G0 (V^2/Hz):", G0)
    print("Estimated ENBW B (Hz):", B)
    print("Sigma_mean for total time T (V):", sigma_m)

    # If you have a target sigma_mean:
    target = 1e-9  # 1 nV
    T_need = required_T_for_sigma_mean(G0, target)
    print("Time needed for target sigma_mean (s):", T_need, "  (~hours)", T_need/3600)

fs：读数速率（例如 DMM/纳伏表 1 SPS、10 SPS）
nperseg：决定最低频点 Δf≈fs/nperseg（要到 mHz，就得大）
G0 的估计频带 (f_lo, f_hi)：根据你 PSD 里“白噪声平台”所在区间选

这篇论文的数学价值在于：把“直流测量的玄学经验”，变成“可计算、可复现实验规则”。

8

<完>